「台形の面積公式について」その２
○ 面積の公式以上に大切な 補助線引くこと覚えましょう
|本文エッセー | 狂歌ジンセー論トップ | ＨＰトップ|
MYＣＭ：御影祐の第３弾書籍！(狂短歌＋エッセー)
書 名＝『 狂短歌人生論――本当は愛することより大切な 』
全国書店にて販売中！ ご注文は書店・インターネットで m(_ _)m
☆作者「御影祐」 出版社「本の森」 税込み定価 \ ９９８円
詳細は著書紹介コーナー（その３）で
ゆうさんごちゃまぜＨＰ「狂歌教育人生論」 ２０１１年 ４月２２日（金）第 133号
前号に続いて【台形の面積公式 その２】です。
本文に入る前に、台形の面積＝［（上底＋下底）×高さ÷２］を説明するもう一つの方法があることをお伝えしておきたいと思います。
平行四辺形の面積公式はご存じと思いますが［底辺×高さ］です。
台形の面積公式についてこれを使って説明（証明）しようという方法です。
まず台形ＡＢＣＤと全く同じ大きさの台形をもう一つ作り（ＥＦＧＨとしましょう）、それを逆さにしてＡＢＣＤの右端にくっ付けます。
ＣＤとＨＧが重なると（詳細は省きますが）大きな平行四辺形ＡＢＥＦができあがります。
当然これは台形ＡＢＣＤの２倍の大きさです。
この平行四辺形ＡＢＥＦの底辺は台形ＡＢＣＤの底辺と台形ＥＦＧＨの上辺（＝台形ＡＢＣＤの上辺）が足された長さです。よってこの平行四辺形の面積は［台形ＡＢＣＤの（底辺＋上辺）×高さ］となります。
すると台形ＡＢＣＤはちょうどその半分だから２で割る、つまり［（底辺＋上辺）×高さ÷２］となる……ってわけです(^_^)。
しかしながら、私はこの説明と言うか、証明にあまり納得できません。
と言うのは、この説明では「なぜ上辺なのに、上の底という名を付けたのか」がわからないままだからです。
やっぱり「逆向き三角形の底辺に当たるから上底と名を付けた、二つの三角合体説」がいいと思います(^_^)。
ただ、小学生には逆向き三角形――頂点が底辺を飛び出した形の三角形でも、その面積は［底辺×高さ÷２］であることを納得させる（証明する）必要があり、それはちょっと難しすぎるかもしれません。
この件は長くなるので最後に別項として解説しました。
さて、そこで本稿に入ります。
前号で最後に述べた「最も大切なことは台形に補助線を引いて二つの三角形に分けたことで、これこそ算数・数学の基本中の基本で、面積の公式を覚えること以上に、最も重要なこと」についてのうんちくです(^_^)。
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−(^_^)本日の狂短歌(^_^)
○ 面積の公式以上に大切な 補助線引くこと覚えましょう
(^O^) ゆとりある人のための10分エッセー (^O^)
【 台形の面積公式 その２ 】
前号では台形について詳しく述べましたが、小学校では面積公式として他に正方形・長方形・三角形・平行四辺形も学ぶはずです。
その公式は以下の通りです。
１ 正 方 形＝タテ×ヨコ
２ 長 方 形＝タテ×ヨコ
３ 三 角 形＝底辺×高さ÷２
４ 平行四辺形＝底辺×高さ
５ 台 形＝（上底＋下底）×高さ÷２
私のかすかな記憶では「それぞれの図形の性質を教わり、そして各数値が示され、それを計算して面積を出す」練習が何度か繰り返されたような気がします。
先生が台形の「上底」の意味を教えてくれたか。あるいは三角形の意味とか「この面積公式全体で最も大切なことは何か……」などを教えてくれたか、記憶にありません(^_^;)。
しかし、私は懇意にしている数学の先生と話し合うことで「公式を覚えることが大切なのではない。算数・数学の基本をしっかり勉強して、それをいろいろな問題で応用できる力を身につけることが大切なんだ」と知りました。
なぜなら公式はそのうち忘れてしまう。しかし、忘れても「公式の意味さえしっかり理解していれば、自力で作り出すことができる」からです。公式の意味を理解すること――それが数学の基本です。
そして三角形・四角形の面積公式において最も大切なことは、台形でやったように《補助線を引くこと》なのです。
公式を忘れても、補助線を引ければ面積公式を思い出せるし、作り出せる。
また、補助線を引ければ、公式を思い出せなくても計算して答えを出すことができる。
何よりも出題された問題を投げ捨てることなく、挑戦することができる。
前号のように――台形の公式を忘れても、対角線に補助線を引いて「三角形が二つだから、それを足して答えを出そう」と挑戦することができるのです。
たとえば、優等生――と言うか記憶力のいい子は台形の面積公式を覚えていられるし、それを使ってすらすら答えが出せるでしょう。当然満点です。
しかし、劣等生――と言うか記憶力の良くない子は台形の面積公式を忘れるから、答えが出せません。解こうともしないので０点です。
しかし、公式を忘れても《台形の公式暗記するよりも 三角二つ足せば良し》を思い出せれば、ちょっと時間がかかろうとも、優等生同様正解にたどりつけます。
まー優等生がウサギで、こちらのやり方はカメの歩みかもしれませんが(^.^)。
しかし、問題を解くために補助線を引く――補助線を引いて問題を解く――というのは面積公式以上に大切な算数・数学の基本なのです。
三角形・平行四辺形・台形の公式は忘れる可能性があります。忘れてしまうと、中学・高校になってその系統の問題が出題されたらお手上げです。
しかし、公式を忘れても、補助線さえ引ければ公式を思い出せるし、何より問題に挑戦して答えを出すことができます。
これは大げさに言うなら、社会に出たとき自分が持つ知識や考える力を総動員して様々な課題・トラブルに挑戦する――その力を養うことでもあります。大切なことは「できないや、とあきらめる」ことではなく「挑戦すること」なのです。
それでは、この基本中の基本から四角形・三角形の面積公式を見直してみましょう。
まず正方形・長方形ですが、この公式［タテ×ヨコ］は単純だからまず忘れません(^.^)。
私は正方形・長方形の面積公式は「タテ×ヨコ」だけでなく［底辺×高さ］としても覚えた方がいいと思っています。
ヨコとは底辺であり、タテとは高さであると。
小学生を相手とするなら、正方形や長方形をノートに書いて、タテ・ヨコ１センチ刻みに点を付け、ものさしで計ってそれがタテ・ヨコ全て同じ長さだと確認すればいいでしょう。
つまり、
１ 正方形の面積＝［タテ×ヨコ］＝［底辺×高さ］
２ 長方形の面積＝［タテ×ヨコ］＝［底辺×高さ］……と言い換えておくわけです。
こうした方が残りの面積公式が簡単になります。
すると、三角形の面積公式は、仮に公式を忘れても、正方形や長方形に補助線として対角線を１本引くことで思い出せます。
つまり、三角形は「正方形や長方形に補助線として対角線を１本引くだろ。そうすると直角三角形が二つできる。この二つの三角形は全く同じ大きさだ。
だから三角形の面積は正方形・長方形の半分だから＝［タテ×ヨコ］÷２＝［底辺×高さ÷２］だ」となります(^_^)。
３ 三角形＝［正方形・長方形の半分］＝［底辺×高さ÷２］
そして、平行四辺形も「補助線として対角線を１本引くだろ。すると三角形が二つできる。底辺と高さは二つとも全く同じ。だから、平行四辺形＝二つの三角形の２倍＝底辺×高さ÷２×２＝底辺×高さ」となる。
４ 平行四辺形＝同じ三角形が二つ＝底辺×高さ÷２×２＝底辺×高さ
最後に台形も「補助線１本で、下の三角形と上の逆向き三角形の二つができる。だから大小二つの三角形の面積を足せばいい＝底辺×高さ÷２＋上の辺×高さ÷２だ」となるわけです。
５ 台形＝大小二つの三角形＝底辺×高さ÷２＋上辺×高さ÷２
こうなると、面白いことに《全ての四角形は三角形の合体である》ことに気づきます。
ならば、面積公式の順番は三角形をトップとして以下のように置き換えてみてはどうでしょうか。
１ 三角形 ＝正方形・長方形の半分＝底辺×高さ÷２
２ 正方形＝同じ直角三角形が二つ＝底辺×高さ÷２×２
３ 長方形＝同じ直角三角形が二つ＝底辺×高さ÷２×２
４ 平行四辺形＝同じ三角形が二つ＝底辺×高さ÷２×２
５ 台 形＝大小二つの三角形＝底辺×高さ÷２＋上辺×高さ÷２
［＝］の右（右辺）には全て［底辺×高さ÷２］があります。四角形の基本は三角形なのです。
正方形も長方形も平行四辺形の面積も、三角形を基準に考えれば［底辺×高さ÷２×２＝底辺×高さ］であり、台形も大小二つの三角形を足せばいいとわかるのです。
そして《四角形の面積や図形を解く問題が出題されたら、補助線を引いてできるだけ三角形を作り出す》――これがここでの大切な基本です。面積公式をただ丸暗記するより、もっと大切な算数・数学の基本なのです。
この基本さえ知っていれば、見たことのない応用問題が出てきても、問題に挑戦できるし、解ける可能性があります。
応用問題に挑戦できる力こそ、算数・数学の真の力であると言えるのです。
それでは以上の理屈を駆使して算数・数学の定番――応用問題をやってみましょう(^.^)。
応用問題 （ピタゴラスの定理を学んだ中学生以上対象）
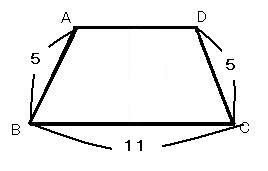１ 台形ＡＢＣＤの底辺ＢＣが１１センチ、斜辺ＡＢ＝ＣＤ＝５センチのとき、この台形の面積を求めなさい（図は正確ではありません）。
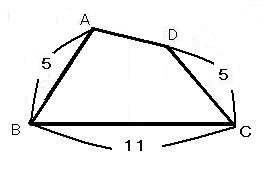２ 台形ではない四角形ＡＢＣＤの底辺ＢＣが１１センチ、斜辺ＡＢ＝ＣＤ＝５センチのとき、この四角形の面積を求めなさい（図は正確ではありません）。
ちなみに、１は台形の公式を覚えていても、上辺（上底）と高さが不明です。それを出さねばなりません。また２は台形ではありません。斜辺が５のとき直角三角形ピタゴラスの定理から他の２辺の長さを出せたとしても、「補助線を引いて解く」基本を知らないと、お手上げかもしれません(^.^)。
《 解 き 方 》
二つの四角形の問題は、補助線を引いて三角形をいかに作り出せるか――それにかかっています。
１、２とも前提としてピタゴラスの定理（直角三角形はａの２乗＋ｂの２乗＝ｃの２乗）であり、斜辺が５センチの特異な三角形は［３・４・５（３の２乗＋４の２乗＝５の２乗）］であることを思い出さないといけません。
それが出てくれば、後は補助線をいかに引くかです。しかし、この場合は対角線ではありません(^.^)。
１の場合は以下の通りです（単位の平方センチは省略します）。
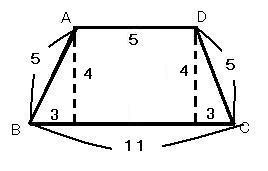まず斜辺５より、他の辺は［３・４］の直角三角形であると計算できれば、すぐに三角形が二つできることに気づきます。つまり、頂点Ａと頂点Ｄから下の辺に垂直に補助線を引くことになります。
すると台形ＡＢＣＤは真ん中の長方形とその左右に二つの直角三角形がある形となります。
この三角形はともに底辺３、高さ４、斜辺５で同じ大きさの三角形です。
真ん中の長方形の底辺は［１１−３−３＝５］だから５センチ、高さは４センチ。長方形の底辺５センチはそのまま上底の長さでもあります。
これで台形の底辺１１、上底５、高さ４が出ます。
よって台形の面積公式を使えば、
面積＝（５＋１１）×４÷２＝１６×４÷２＝３２
カメの方法［同じ三角形二つ＋真ん中の長方形］で計算すれば、
面積＝３×４÷２×２＋５×４＝１２＋２０＝３２
これで得意顔で「計算終了！」――とすると、得点は半分です(^.^)。
この問題はちょっとしたひっかけにもなっており「なお答えは一つと限らない」と書けば、気づいたかもしれません。
台形は斜辺の長さ５センチとしか書いていないのだから、他の辺は［３・４］の場合と［４・３］の場合があります。上記は三角形の底辺３、高さ４として計算しましたが、もう一つ三角形の底辺４、高さ３の場合があるのです。
だから、もう一つは高さ３センチ（上底は１１−４−４で３センチ）の台形です。
よって台形の面積公式を使えば上底３、下底１１、高さ３だから、
面積＝（３＋１１）×３÷２＝２１）
カメの方法［同じ三角形二つ＋真ん中の長方形］で計算すれば、
面積＝４×３÷２×２＋３×３＝１２＋９＝２１
よって正しい答えは［高さ４センチの場合＝３２平方センチ、高さ３センチの場合＝２１平方センチ］となります。
これで満点(^_^)。
次に２の問題です。
台形ではない四角形ＡＢＣＤは１の応用ですが、台形ではないのだから、台形の面積公式は使えません。これこそ歩みののろいカメの方法でないと解けません。
こちらは補助線を３本引いて三角形を三つ作らねばならないのです。
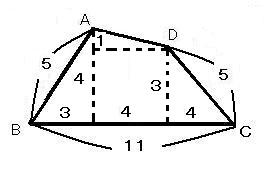それは頂点Ａより下に垂直におろす直角三角形、頂点Ｄより下におろす直角三角形。これは１と同じです。そして、もう一つは頂点Ｄから底辺と平行に左に延ばすことによってできる最上部の小さな直角三角形――この三つです（図は相当いいかげんです(^_^;)。
台形ではないのだから、左のＡを頂点とする三角形を底辺３、高さ４とすると、右の頂点Ｄを頂点とする直角三角形は底辺が４で高さが３になります（逆パターンでも形は同じ）。
すると真ん中の長方形の底辺は［１１−３−４＝４］で４、高さは３。
二つの三角形は底辺×高さ÷２で計算できます。形は違うけれど同じ大きさです。
残る上部の小さな三角形は底辺が長方形と同じだから４。高さは［４−３＝１］で１。
これでこの四角形ＡＢＣＤのうち、三つの三角形と一つの長方形の数字が全て出揃いました。
よって四角形ＡＢＣＤの面積は［三つの三角形＋一つの長方形］で
面積＝３×４÷２＋４×３÷２＋４×１÷２＋４×３
＝６＋６＋２＋１２＝２６（平方センチ） ……となります。
こちらはカメの方法でなければ解けません。台形の面積公式を使うことはなく、補助線を引くこと、三角形を作ってその面積を合計する方法でようやく解くことができました。
解法の解説では台形・四角形の真ん中を長方形としましたが、そこも対角線で二つに分けて全て三角形にしても、構わないわけです。もっと複雑な多角形の場合、そうした方が良いこともあるでしょう。とにかく基本は補助線、そして三角形を作ること――なのです。
ここで、台形の面積公式を使おうとすると、大変なことになって最終的に解けないと思います。
のんびり三角形一つ一つを計算するカメのようなやり方がウサギに勝つのです(^_^)。
次号は最終回として、私がどうしてこのような算数の実戦問題を取り上げるつもりになったか、そのことについてお話ししたいと思います。
○ 面積の公式以上に大切な 補助線引くこと覚えましょう
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
最後まで読んでいただきありがとうございました。
別項：三角形の面積公式について（関心のある方はお読み下さい）
小学校では三角形ＡＢＣの面積を勉強するとき、頂点Ａが底辺ＢＣ内にある三角形はやるでしょうが、ＡがＢＣの外側に出た横長三角形については（その面積も底辺×高さ÷２）勉強しないかもしれません。
となると台形の面積公式で「上の逆向き三角形の面積」という説明は違和感をもたれる可能性があります。
また、今号で《正方形・長方形の対角線に補助線を引けば、同じ大きさの直角三角形二つができる。だから三角形の面積は底辺×高さの半分》とざっくり説明しましたが、
「そんなに単純じゃないだろう」とお叱りを受けるかもしれません(^_^;)。
私としてはあくまで三角形の面積公式を忘れたときの《思い出し方法》のつもりでしたが、以下この件について説明（証明）したいと思います。
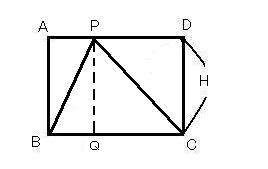たとえば長方形ＡＢＣＤがあるとして、上辺ＡＤ上のどこかに点Ｐを付け、そこから頂点ＢとＣに線を伸ばすと、三角形ＰＢＣができます。
Ｐが上辺のどこにあろうと、三角形ＰＢＣは長方形ＡＢＣＤの半分の面積である――それをまず証明したいと思います。
面白いことに、この証明問題もまた［図形問題では補助線を引く］基本中の基本にのっとって解くことができます。
それは頂点Ｐから下辺ＢＣに垂直に補助線を引くことです。
底辺ＢＣと交わる点をＱとすると長方形ＡＢＣＤには、ＡＢＱＰとＰＱＣＤ二つの長方形ができます。その中の対角線にできた直角三角形はそれぞれの長方形の半分の大きさです。
ということは（中間を省略しますが）三角形ＰＢＣは長方形ＡＢＣＤの半分となることがわかります。Ｐが上辺ＡＤのどの位置にあろうと、必ず半分の面積になるのです。
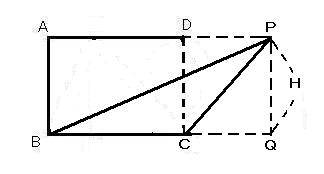もう一つ長方形ＡＢＣＤの上辺ＡＤを（底辺に平行に）右に延長して点Ｐを付けたとします。そのＰとＢ・Ｃを結ぶ線を引くと、えらい傾いた三角形ＰＢＣができます（台形の上辺を底辺とする逆向き三角形がこの形です）。
この三角形ＰＢＣも長方形ＡＢＣＤの半分の面積であることを証明せねばなりません。さて、これはどうするのでしょうか(^_^)？
これもまた頂点Ｐから底辺に垂直な補助線を引き、底辺ＢＣを右に延長して交わった点をＱとします。
すると直角三角形ＰＢＱができます。
三角形ＰＢＣの面積は直角三角形ＰＢＱの面積から直角三角形ＰＣＱの面積を引いたものだとわかります。
［三角形ＰＢＣ＝直角三角形ＰＢＱ−直角三角形ＰＣＱ］
そこで、直角三角形ＰＢＱの面積と直角三角形ＰＣＱの面積を求めると
直角三角形ＰＢＱ＝底辺×高さ÷２＝ＢＱ×ＰＱ÷２
直角三角形ＰＣＱ＝底辺×高さ÷２＝ＣＱ×ＰＱ÷２
ですが底辺の長さＢＱはＢＣ＋ＣＱです。
よって［直角三角形ＰＢＱ−直角三角形ＰＣＱ］は
＝ＢＱ×ＰＱ÷２−ＣＱ×ＰＱ÷２
＝（ＢＣ＋ＣＱ）×ＰＱ÷２−ＣＱ×ＰＱ÷２となります。
この（ ）を消してしまうと、
＝ＢＣ×ＰＱ÷２＋ＣＱ×ＰＱ÷２−ＣＱ×ＰＱ÷２＝ＢＣ×ＰＱ÷２
ＢＣは三角形の底辺、ＰＱは＝ＣＤであり、つまり長方形ＡＢＣＤの高さ＝三角形ＡＢＣの高さ［Ｈ］です。
結局、残ったのは［ＢＣ×ＰＱ÷２］であり、これは三角形ＡＢＣの［底辺×高さ÷２］なのです。
これで横長三角形ＰＢＣの面積も［底辺×高さ÷２］であることがわかります。
もっとも、これは中高生向きの証明で、小学生にはとても向かないと思います(^_^;)。
小学生相手には、あくまで実戦でやるしかないのかなと思います。
たとえば以下のような流れです（センチは省略）。
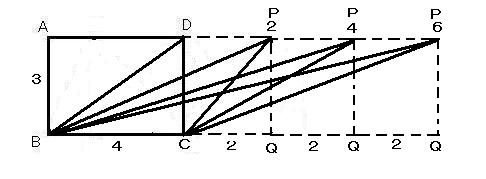底辺４・高さ３の長方形ＡＢＣＤを書き、上辺の延長線上に２・４・６三つの点Ｐを付ける。
まず対角線を引いた直角三角形ＤＢＣの面積は［底辺×高さ÷２］だから、
＝４×３÷２＝６
三角形ＰＢＣの面積は三角形ＰＢＱ−三角形ＰＣＱだから、２・４・６三つの頂点について三角形ＰＢＣの面積を計算してみるのです。
点Ｐが２の場所＝（４＋２）×３÷２−２×３÷２
点Ｐが４の場所＝（４＋２＋２）×３÷２−（２＋２）×３÷２
点Ｐが６の場所＝（４＋２＋２＋２）×３÷２−（２＋２＋２）×３÷２
これをそれぞれ計算すると
点Ｐが２の場所＝ ９−３＝６
点Ｐが４の場所＝１２−６＝６
点Ｐが６の場所＝１５−９＝６ ……と全て同じ数になります。
つまり、点Ｐが延長線上のどこにあろうと、結果は長方形ＡＢＣＤの半分の面積に等しいというわけです(^_^)。
この説明も「小学生には難しすぎる」となると、《台形の面積は下の三角形と上の逆向き三角形の面積を足したもの》という説明（証明）そのものが不可能になってしまいます。要するに、台形の逆向き三角形は必ず横長三角形になるからです。
この横長三角形の面積も［底辺×高さ÷２］であることを小学生に納得させなければなりません。
その説明が難しすぎるというのであれば、台形の面積公式は小学校では教えられない――という結論になるのかもしれません。
少なくとも「上底」の意味を理解するためには、どうしても逆向き三角形を出さざるを得ないからです。
以上です。（御影祐）
狂歌今日行くジンセー論 トップ
ＨＰトップ
Copyright(C) 2011 ＭＩＫＡＧＥＹＵＵ．All rights reserved.